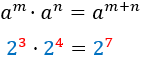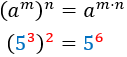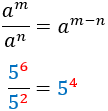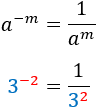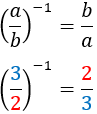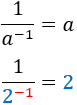Propiedades de las raíces enésimas | CURSO ONLINE DE MATEMÁTICAS

En esta página definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos sus propiedades. Después, aplicamos la teoría vista para simplificar expresiones algebraicas con raíces.

Nota 1: trabajamos con raíces de distintos órdenes (cuadrada, cúbica, cuarta, quinta, etc.).

Nota 2: sólo consideramos las raíces reales.

1. Introducción y definiciones

Escribir las raíces como potencias nos permite aplicar las propiedades de las potencias (las recordamos en el siguiente apartado). Esto es muy útil para calcular productos y cocientes de raíces e, incluso, potencias y raíces de raíces.

A continuación, recordamos los conceptos y propiedades que necesitamos.

Raíz de orden $n$ :

Sea $n$

un natural positivo (es decir, 1, 2, 3, …), entonces

La raíz de orden $n$

(o raíz

n

-ésima) del número

a

es el número

b

que cumple

b^{n} = a

Es decir,

b^{n} = a

\sqrt[n^]{a} = b \Leftrightarrow {b^}^{n} = a

b^{n} = a

El número $n$ es el orden de la raíz y el número $a$ es su radicando. El número $b$ es la raíz n-ésima de $a$ .

Importante:

Si el orden de la raíz, $n$ , es par, su radicando tiene que ser mayor o igual que 0. Además, si el radicando es mayor que 0, hay dos raíces: una positiva y una negativa. $n$

Por ejemplo, las raíces cuadradas de 4 son 2 y -2:

$Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$
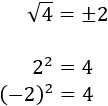
Si el orden de la raíz, $n$ , es impar, su radicando puede ser negativo. Además, en este caso ( $n$ impar), sólo hay una raíz. $n$

Por ejemplo, la raíz cúbica de 8 es 2 y la de -8 es -2:

$Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$

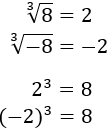
Raíz escrita como potencia:

Podemos escribir la raíz $\sqrt[n]{a}$

como la potencia con base

a

y exponente

1 / n

1 / n

$\sqrt[n^]{a} = {a^}^{\frac{1/}{n}}$

2. Propiedades de las potencias

Recordamos las propiedades básicas de las potencias.

Ver propiedades

Producto $Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$	Potencia $Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$
Cociente $Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$	Exponente negativo $Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$
Inverso $Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$	Inverso $Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$

3. Propiedades de las raíces

Si escribimos las raíces como potencias, obtenemos las siguientes propiedades:

Producto de raíces:

$Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$

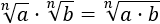
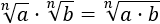
El producto de raíces (del mismo orden) es la raíz del producto de sus radicandos.

Cociente de raíces:

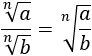
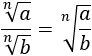
El cociente de raíces (del mismo orden) es la raíz del cociente de sus radicandos.

Potencia de una raíz:

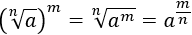
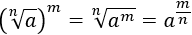
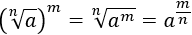
Podemos introducir el exponente de una raíz como el exponente del radicando.

Raíz de una raíz:

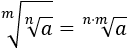
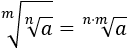
La raíz de orden $m$ de la raíz de orden $n$ es la raíz de orden $m \cdot n$ . $m \cdot n$

Nota: en el Ejercicio 5 tenemos otras dos propiedades.

4. Ejercicios resueltos

Nota previa: cuando haya dos raíces, escribiremos sólo la positiva.

En todos los ejercicios se tiene que simplificar el resultado.

Ejercicio 1

Calcular los siguientes productos de raíces cúbicas y quintas:

Solución

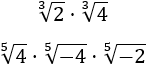
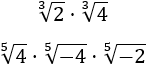
Aplicamos la propiedad del producto de raíces.

Primer producto:

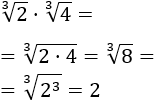
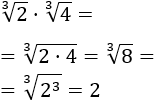
Observen que la raíz se cancela porque el radicando es una potencia con exponente 3 y el orden de la raíz es 3.

Segundo producto:

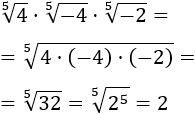
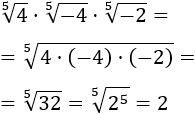
La raíz se cancela por la misma razón que en producto anterior.

Ejercicio 2

Calcular los siguientes cocientes de raíces cuadradas y cúbicas:

Solución

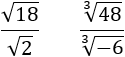
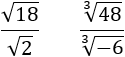
Aplicamos la propiedad del cociente de raíces.

Primera división:

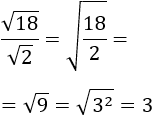
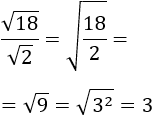
Segunda división:

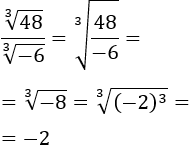
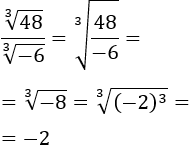
Ejercicio 3

Calcular el siguiente cociente de raíces cuadradas y cúbicas:

Solución

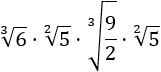
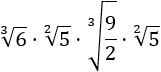
Observen que no todas las raíces tienen el mismo orden.

Como tenemos un producto de raíces y el producto conmuta, podemos cambiar el orden:

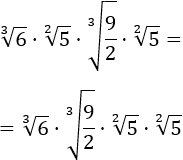
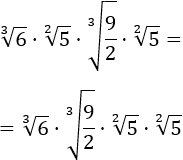
Así, podemos multiplicar las dos raíces de la izquierda y las dos de la derecha porque tienen el mismo orden:

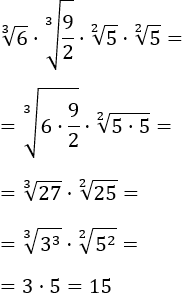
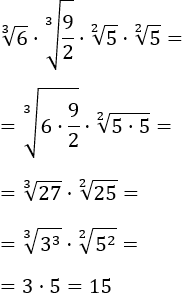
Ejercicio 4

¿La suma de raíces de orden $n$ es la raíz de orden $n$ de la suma de sus radicandos? $n$

Solución

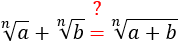
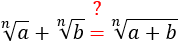
La propiedad no es cierta. Veamos un contraejemplo:

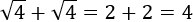
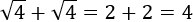
Sin embargo,

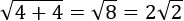
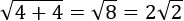
Ejercicio 5

Demostrar las siguientes propiedades:

Propiedad 1:

$Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$
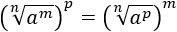
Propiedad 2:

$Definimos las raíces como potencias cuyos exponentes son fracciones y proporcionamos las propiedades de las raíces (producto de raíces, cociente de raíces, potencia de una raíz...). Resolvemos ejercicios y problemas de calcular y simplificar expresiones algebraicas con raíces. Matemáticas. Secundaria, ESO. Bachillerato. Cálculo.$

Solución

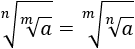
Vamos a operar en el lado izquierdo hasta transformarlo en la expresión del lado derecho.

Propiedad 1:

Escribimos la raíz como una potencia:

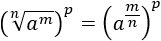
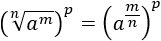
Multiplicamos los exponentes (potencia de potencia):

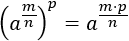
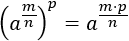
Hacemos el paso inverso:

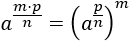
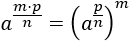
Escribimos la potencia como una raíz:

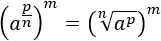
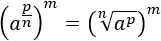
Propiedad 2:

Escribimos las raíces como potencias:

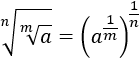
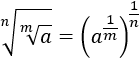
Multiplicamos los exponentes:

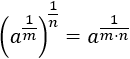
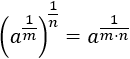
Ahora, deshacemos el cambio:

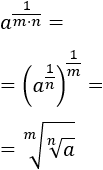
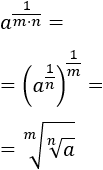
En adelante, lo que haremos es escribir las raíces como potencias con exponente fraccionario para aplicar las propiedades de las potencias.

Ejercicio 6

Calcular la siguiente potencia:

Solución

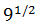
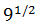
Tenemos una raíz cuadrada escrita en forma de potencia:

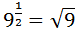
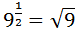
Sabemos que la raíz cuadrada de 9 es 3, pero podemos escribir 9 como $3^{2}$ para dejar claro en la raíz cuadrada de un cuadrado se pueden eliminar la raíz y el exponente:

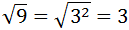
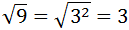
Ejercicio 7

Escribir la potencia como una raíz:

Solución

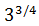
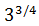
Recuerden la propiedad:

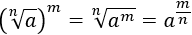
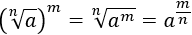
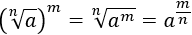
Como el denominador del exponente es 4, es una raíz de orden cuarto (raíz cuarta):

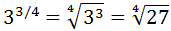
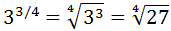
No podemos simplificar más la raíz.

Ejercicio 8

Escribir la siguiente potencia como una raíz:

Solución

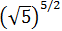
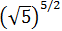
Escribimos la raíz cuadrada como una potencia (con exponente 1/2):

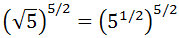
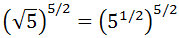
Como tenemos un potencia de una potencia, multiplicamos los exponentes:

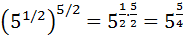
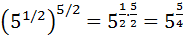
Escribimos la potencia como una raíz:

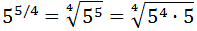
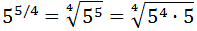
Como la raíz es cuarta, podemos extraer un 5 por cada $5^{4}$ del radicando:

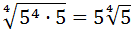
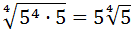
Ejercicio 9

Simplificar:

Solución

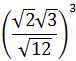
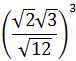
Aplicamos la propiedad del producto de raíces del mismo orden:

Aplicamos la propiedad del cociente de raíces del mismo orden:

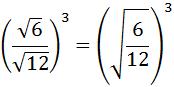
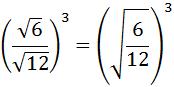
Simplificamos la fracción:

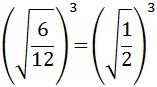
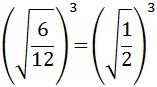
Simplificamos más:

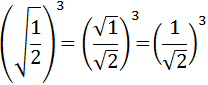
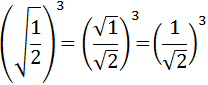
La potencia de un cociente es el cociente de sus potencias:

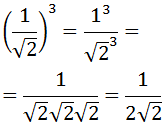
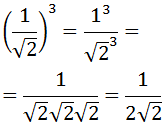
Podemos dejar el resultado así, pero a los matemáticos no nos gustan las raíces en los denominadores. Para evitar esto, multiplicamos y dividimos por la raíz del denominador:

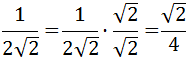
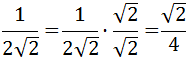
Ejercicio 10

Escribir como una raíz:

Solución

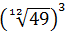
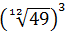
Escribimos la raíz de orden doce como una potencia y simplificamos el exponente:

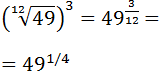
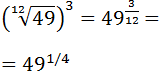
Observen que hemos pasado de una raíz de orden 12 a una de orden 4. Escribimos el radicando, 49, como una potencia. Es decir, cambiamos 49 por $7^{2}$ . Así, podemos aplicar la propiedad de la potencia de una potencia:

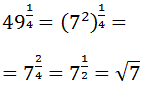
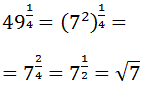
Ejercicio 11

Calcular:

Solución

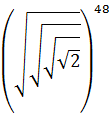
Tenemos raíces cuadradas anidadas. Vamos a escribir todas ellas como potencias con exponente 1/2. Después, podemos multiplicar los exponentes (potencia de una potencia):

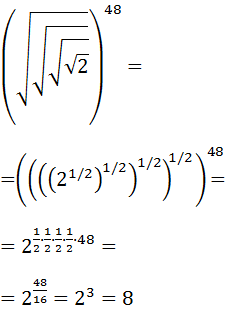
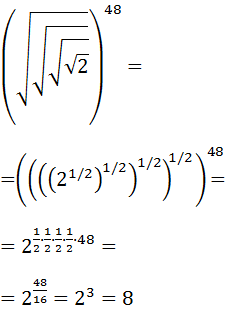
Ejercicio 12

Escribir en forma de raíz:

Solución

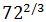
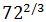
Escribimos 72 como un producto de potencias para aplicar la propiedad de la potencia de un producto:

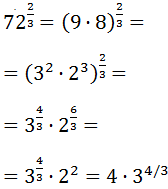
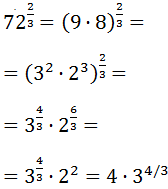
Escribimos la potencia fraccionaria como una raíz cúbica para extraer algún factor:

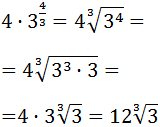
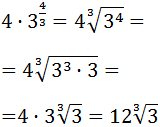
Observen que, como tenemos una raíz cúbica, podemos extraer un 3 por cada $3^{3}$ del radicando (sólo había uno).

Ejercicio 13

Escribir como una raíz:

Solución

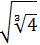
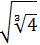
Escribimos la raíz cúbica como una potencia con exponente $1 / 3$ y la raíz cuadrada como una potencia con exponente $1 / 2$ : $1 / 2$

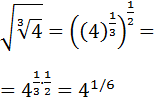
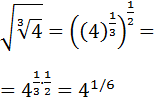
Escribimos el radicando, 4, como un potencia, $2^{2}$ :

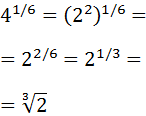
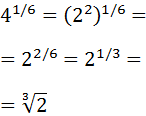
Ejercicio 14

Calcular:

Solución

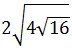
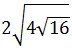
Transformamos las raíces cuadradas en potencias y escribimos el número 4 como $2^{2}$ y el número 16 como $2^{4}$ . Después, aplicamos las propiedades de las potencias:

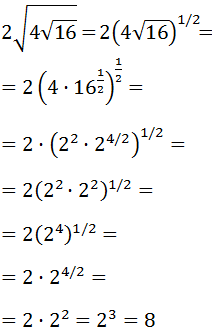
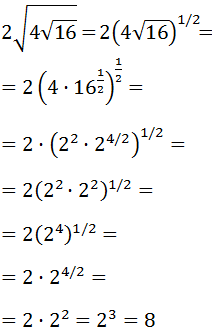
Ejercicio 15

Simplificar:

Solución

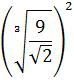
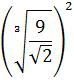
Escribimos 9 como la potencia $3^{2}$ y las raíces cúbica y cuadrada como potencias con exponentes $1 / 3$ y $1 / 2$ :

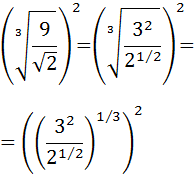
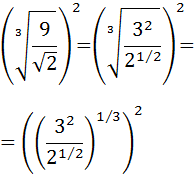
Como tenemos potencias de potencias, sólo tenemos que multiplicar los exponentes:

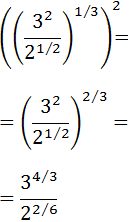
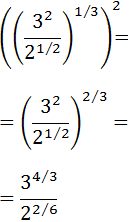
Simplificamos y escribimos como raíz:

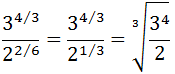
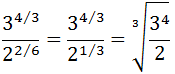
Hemos escrito el resultado como una raíz para extraer un factor de la raíz:

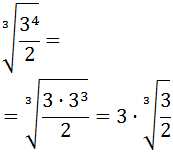
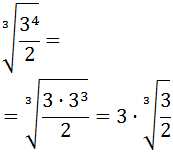
Si queremos, podemos seguir operando hasta llegar al resultado

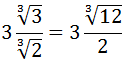
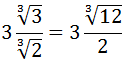
Ejercicio 16

Calcular:

Solución

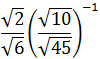
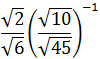
Recordemos que la potencia -1 de una fracción es la fracción inversa (cambiar denominador por numerador):

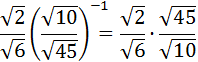
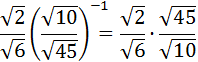
El producto de fracciones se calcula multiplicando entre sí los númeradores y los denominadores:

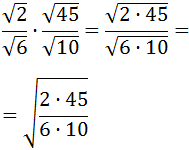
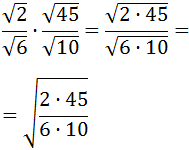
Simplificamos la fracción del radicando:

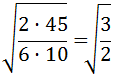
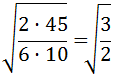
Eliminamos la raíz del denominador multiplicando y dividiendo por la raíz de 2:

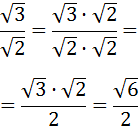
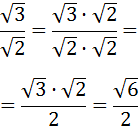
Ejercicio 17

Calcular:

Solución

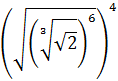
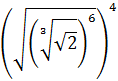
Sólo tenemos que escribir las raíces como potencias para multiplicar los exponentes (potencia de potencia):

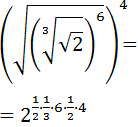
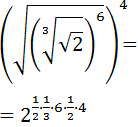
Simplificamos el exponente:

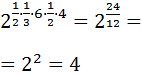
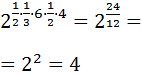
Ejercicio 18

Escribir en forma de raíz:

Solución

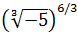
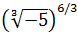
No es un problema que el radicando sea negativo porque la raíz es de orden impar.

Escribimos la raíz cúbica como una potencia:

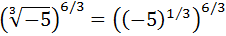
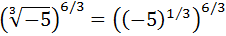
Multiplicamos los exponentes:

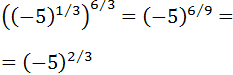
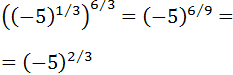
Podemos eliminar el signo negativo porque $(- 5)^{2} = 5^{2}$ :

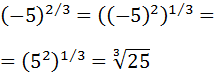
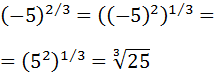
Ejercicio 19

Calcular:

Solución

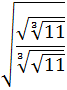
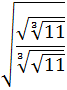
Escribimos las cinco raíces como potencias:

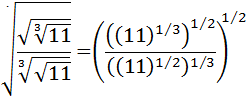
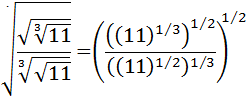
Multiplicamos exponentes:

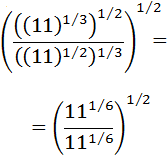
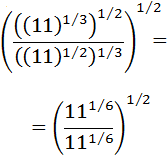
El cociente de potencias es 1 porque el numerador y el denominador son iguales:

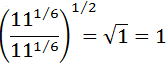
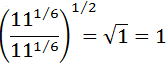
Ejercicio 20

Simplificar:

Solución

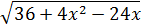
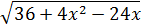
Podemos extraer 4 como factor común:

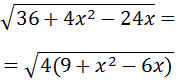
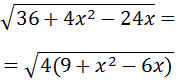
El 4 sale fuera de la raíz cuadrada como 2 porque es $2^{2}$ :

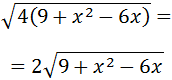
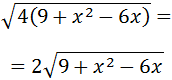
El radicando es el desarrollo del cuadrado de un binomio:

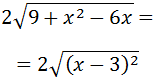
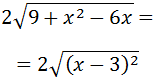
Finalmente, el cuadrado se cancela con la raíz cuadrada:

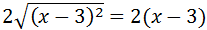
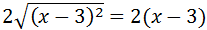
Nota: en realidad, deberíamos escribir valor absoluto al cancelar el cuadrado con la raíz porque el binomio podría tomar valores negativos:

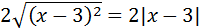
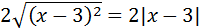
Propiedades de las raíces enésimas | CURSO ONLINE DE MATEMÁTICAS

propiedades de las raíces pdf

raíces enésimas ejemplos

propiedades de las raíces ejercicios

propiedades de las raíces suma

raíces matemáticas

raíces enésimas ejercicios

propiedades de las raíces cuadradas

raíces n-ésimas de números complejos

Te puede interesar:

LA DERIVADA DE UNA FUNCIÓN | CALCULO DIFERENCIAL

¿COMO SIMPLIFICAR FRACCIONES ALGEBRAICAS ? | MATEMÁTICAS

FUNCIONES TRIGONOMÉTRICAS