▷▷✔️ LA HIPÉRBOLA

Tabla de contenidos

LA HIPÉRBOLA | MATEMÁTICAS
PREGUNTAS FRECUENTES SOBRE LA HIPÉRBOLA
Hipérbola como lugar geométrico.
Relación entre los parámetros de la hipérbola a,b y c.
Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados.
Forma de hipérbolas centradas en el origen
Forma de hipérbolas centradas fuera del origen

LA HIPÉRBOLA | MATEMÁTICAS

PREGUNTAS FRECUENTES SOBRE LA HIPÉRBOLA

Una hipérbola es también un lugar geométrico. Definición: Dados dos puntos fijos F y F’, llamados focos y una constante que llamaremos 2a, se llama hipérbola al lugar geométrico de los puntos del plano cuya diferencia de distancia (en valor absoluto) a los dos puntos fijos (F y F’) es constante (2a).

Como puede ver, la gráfica de la hipérbola tiene dos ramales desconectados que se ven similares a las parábolas. Cada ramal se acerca en asíntotas diagonales. El centro de una hipérbola es el punto medio del segmento de línea uniendo sus focos.

Hipérbola como lugar geométrico.

Es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante. PF-PF’=2A

Relación entre los parámetros de la hipérbola a,b y c.

En primer lugar, se dice semieje a la mitad de un eje. Por ejemplo, el semieje real es el segmento que va desde el punto A hasta el centro de la hipérbola, cuya longitud es $a.$

Así pues, existe una relación muy importante entre el semieje real, el semieje imaginario y la semidistancia focal. De hecho, la fórmula que deduciremos a continuación se utiliza bastante para resolver ejercicios y problemas de hipérbolas.

Debes saber que los puntos B y B’ de una hipérbola corresponden a los puntos donde se cruzan el eje principal y la circunferencia imaginaria de radio $c$ (semidistancia focal) con centro en el punto A. En consecuencia, como puedes ver en la siguiente representación gráfica, el segmento que une el punto A y el punto B coincide con el radio de dicha circunferencia ( $c$ ):

De forma que se puede demostrar a partir del teorema de Pitágoras que la relación entre los parámetros $a, b$ y $c$ es la siguiente: $c^2 = a^2+b^2$

Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados.

Una hipérbola es una sección cónica formada por la intersección de un cono doble recto por un plano a un ángulo en el que ambas bases son cortadas. La hipérbola está compuesta de dos ramas que son una reflexión la una de la otra. La hipérbola también es definida como el conjunto de todos los puntos en el plano cartesiano de modo que la diferencia de las distancias entre cualquier punto y los focos es igual a una constante.

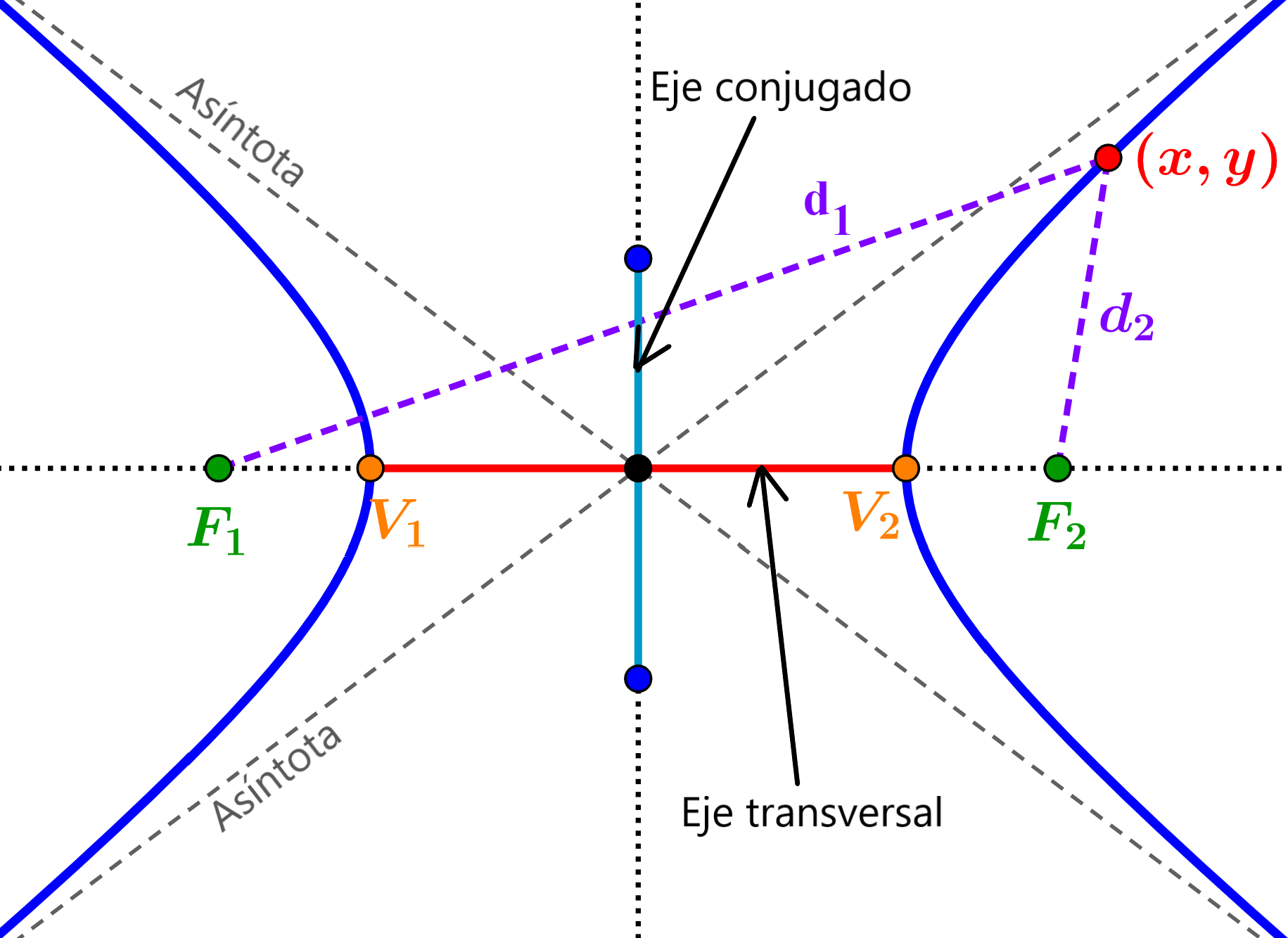
Las hipérbolas tienen dos ejes de simetría. El eje transversal es el segmento que pasa a través del centro y que une a los vértices. Los focos se ubican en la línea que contiene al eje transversal. El eje conjugado es perpendicular al eje transversal y conecta a los cóvertices. El centro es el punto de intersección del eje transversal y el eje conjugado. Las hipérbolas también tienen dos asíntotas, las cuales también intersecan en el centro. LA HIPÉRBOLA | MATEMÁTICAS

Forma de hipérbolas centradas en el origen

La forma estándar de una hipérbola nos da información sobre la ubicación de los vértices y de los focos y de allí podemos definir a la hipérbola completamente. Existen dos variaciones de las ecuaciones de las hipérbolas que tienen al centro en el origen dependiendo en su orientación. Podemos tener hipérbolas posicionadas horizontalmente o verticalmente en el plano cartesiano.

Ecuación de la hipérbola horizontal

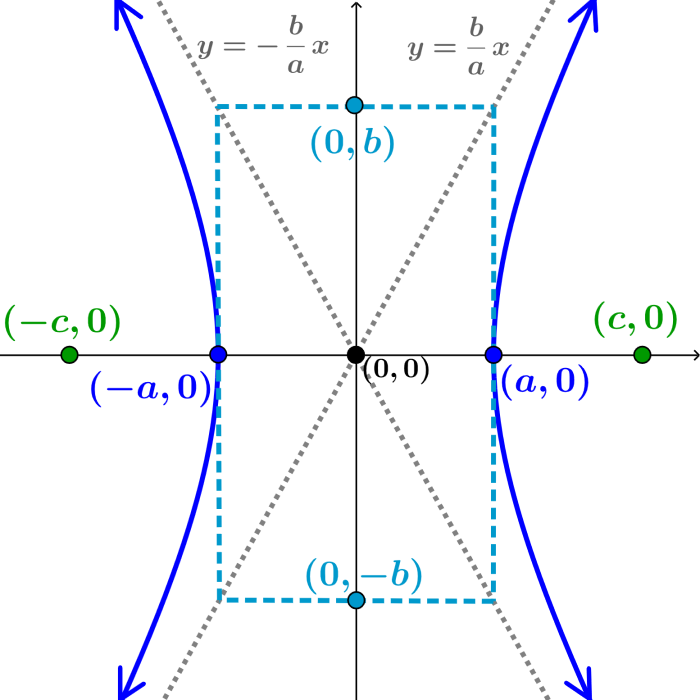
La forma estándar de una hipérbola que tiene al centro en (0, 0) y en la que su eje trasnversal está en el eje x es:

$\frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$

En donde,

$2a$ es la longitud del eje transversal (segmento que une a los vértices)
Las coordenadas del vértice son $(\pm a, 0)$
$2b$ es la longitud del eje conjugado (segmento que une a los covértices)
Las coordenadas de los covértices son $(0, \pm b)$
$2c$ es la distancia entre los focos
Encontramos a c usando ${{c}^2}={{a}^2}+{{b}^2}$
Las coordenadas de los focos son $(\pm c, 0)$
Las ecuaciones de las asíntotas son $y=\pm \frac{b}{a}x$

Ecuación de la hipérbola vertical

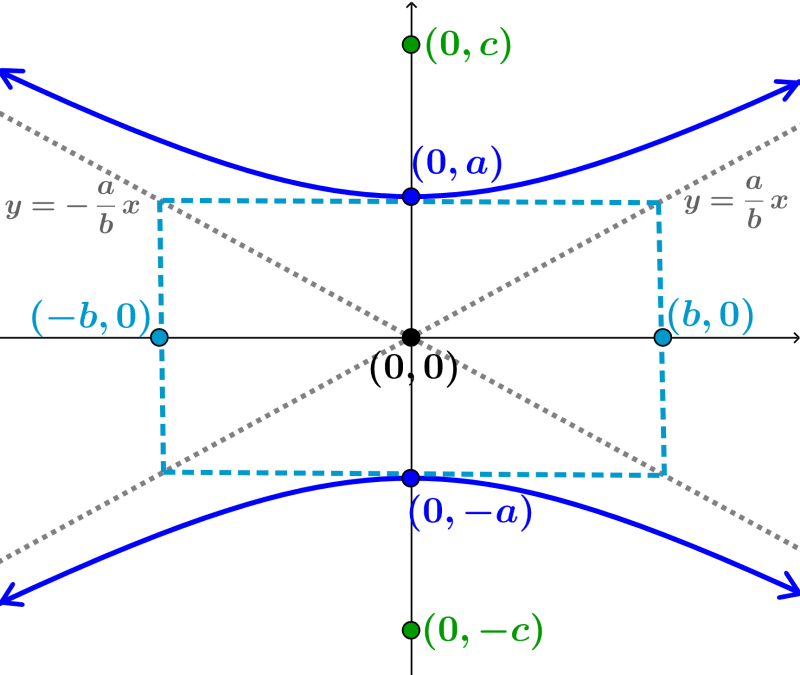
Cuando la hipérbola tiene al centro en el origen, (0, 0), y su eje trasnversal es el eje y, su ecuación es:

$\frac{{{y}^2}}{{{a}^2}}-\frac{{{x}^2}}{{{b}^2}}=1$

En donde,

$2a$ es la longitud del eje transversal
Las coordenadas del vértice son $(0, \pm a)$
$2b$ es la longitud del eje conjugado
Las coordenadas de los covértices son $(\pm b, 0)$
$2c$ es la distancia entre los focos, en donde, ${{c}^2}={{a}^2}+{{b}^2}$
Las coordenadas de los focos son $(0, \pm c)$
Las ecuaciones de las asíntotas son $y=\pm \frac{a}{b}x$

Formas ordinaria y general de la ecuación de la hipérbola con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados.

Las hipérbolas son definidas como secciones cónicas que son obtenidas cuando un cono doble es intersecado por un plano. La hipérbola es formada cuando el plano corta a ambas caras del cono. La hipérbola contiene dos ramas que tienen una forma de parábola y que son la reflexión la una de la otra. El conjunto de todos los puntos en una hipérbola se caracterizan porque la diferencia de las distancias entre cualquier punto en la hipérbola y los focos es igual a una constante.

Una hipérbola tiene dos ejes de simetría. El eje transversal se extiende desde un vértice hasta el otro vértice y pasa por el centro. Los focos definen a la hipérbola y se ubican en la línea que contiene al eje transversal. El eje conjugado se extiende desde un covértice hasta el otro y es perpendicular al eje transversal. El punto de intersección del eje transversal y el eje conjugado es el centro de la hipérbola. El centro también es el punto de intersección de las dos asíntotas.

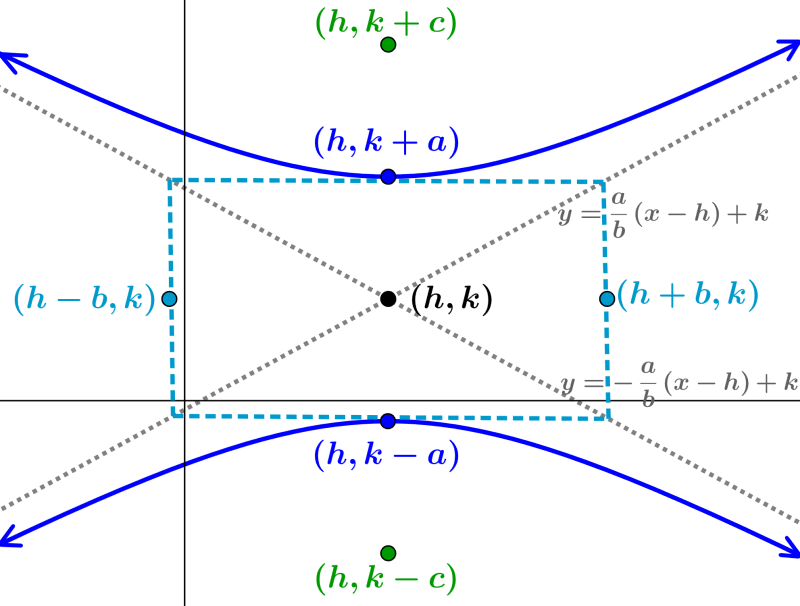
Forma de hipérbolas centradas fuera del origen

La forma estándar de hipérbolas centradas fuera del origen es encontrada al aplicar una traslación de h unidades en el eje x y k unidades en el eje y. Esto resulta en que el centro de la hipérbola esté ubicado en $(h, k)$ . Tenemos dos variaciones de esta ecuación dependiendo en la orientación de la hipérbola.

Ecuación de la hipérbola horizontal con centro fuera del origen

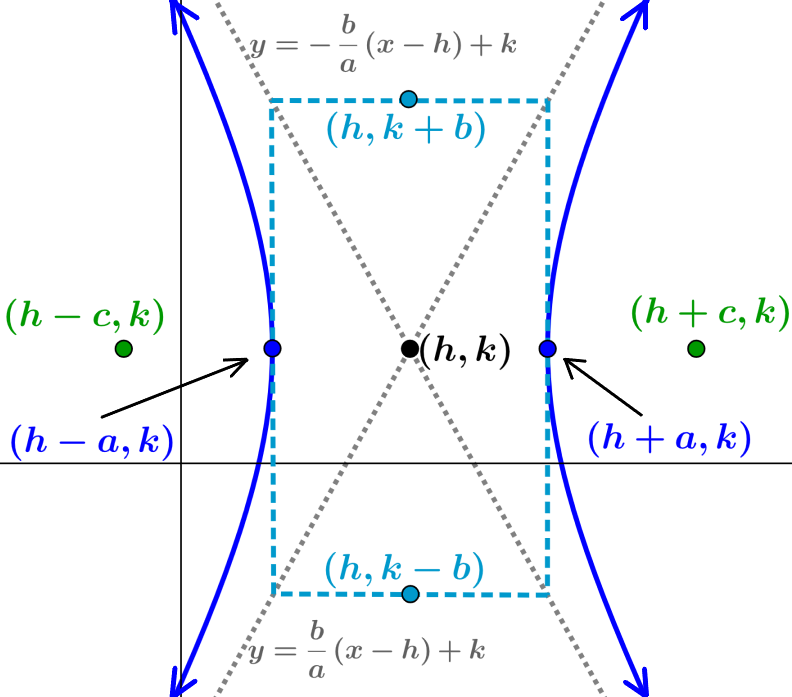
Una hipérbola que tiene al centro en $(h, k)$ y en la que su eje transversal es paralelo al eje x es:

$\frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$

En donde,

h es la coordenada en x del centro y k es la coordenada en y del centro
La longitud del eje transversal es $2a$ (segmento que une a los vértices)
Los vértices están ubicados en $(h\pm a, k)$
La longitud del eje conjugado es $2b$ (segmento que une a los covértices)
Los covértices están ubicados en $(h, k\pm b)$
La distancia entre los focos es $2c$
Encontramos a c usando ${{c}^2}={{a}^2}+{{b}^2}$
Los focos están ubicados en $(h \pm c, 0)$
Las ecuaciones de las asíntotas son $y=\pm \frac{b}{a}(x-h)+k$

Ecuación de la hipérbola vertical con centro fuera del origen

Cuando la hipérbola está centrada en el punto $(h, k)$ y su eje transversal es paralelo al eje y, su ecuación es:

$\frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$

EN DONDE

h es la coordenada en x del centro y k es la coordenada en y del centro
La longitud del eje transversal es $2a$ (segmento que une a los vértices)
Los vértices tienen las coordenadas $(h, k\pm a)$
La longitud del eje conjugado es $2b$ (segmento que une a los covértices)
Los covértices tienen las coordenadas $(h\pm b, k)$
La distancia entre los focos es $2c$ , en donde, ${{c}^2}={{a}^2}+{{b}^2}$
Los focos tienen las coordenadas $(h, k\pm c)$
Las asíntotas tienen las ecuaciones $y=\pm \frac{a}{b}(x-h)+k$

Elementos de una hipérbola.

1. Focos: Son los puntos fijos F y F’.
2. Eje principal o real: Es la recta que pasa por los focos.
3. Eje secundario o imaginario: Es la mediatriz del segmento FF’.
4. Centro: Es el punto de intersección de los ejes.
5. Vértices: Los puntos A y A’ son los puntos de intersección de la hipérbola con el eje focal.
Los puntos B y B’ se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
6. Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF’.
7. Distancia focal: Es el segmento de longitud 2c.
8. Eje mayor: Es el segmento de longitud 2a.
9. Eje menor: Es el segmento de longitud 2b.
10. Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
11. Asíntotas: Son las rectas de ecuaciones:
12. Relación entre los semiejes : c²=a²+b²

CURSO PARA LA UNAM IPN UAM COMIPEMS CENEVAL EXAMEN CULTURAL SEDENA SEMAR

LA HIPÉRBOLA | MATEMÁTICAS

1.elementos de la hipérbola

2.hipérbola ecuación

3.ejes de la hipérbola

4.vértice de la hipérbola

5.asíntotas de la hipérbola

6.propiedades de la hipérbola

7.gráfica de la hipérbola

8.hipérbola ejemplos

LA HIPÉRBOLA | MATEMÁTICAS

Te puede interesar:

MATEFACIL YOUTUBE | CURSO DE MATEMÁTICAS

LEY DE LOS SENOS Y LEY DE LOS COSENOS

Propiedades de las raíces enésimas | CURSO ONLINE DE MATEMÁTICAS

0 0 votes

Article Rating

Gran isla de basura del Pacífico ya tiene 3 veces el tamaño de Francia.

COMO INICIAR SESIÓN EN FACEBOOK

2024 : Como monetizar mi página de FACEBOOK

UNLA – Universidad Latina de América

LEY DE LOS SENOS Y LEY DE LOS COSENOS

APRENDE TODO SOBRE LA SEGUNDA GUERRA MUNDIAL | CURSO ONLINE HISTORIA UNIVERSAL

LOS CUATRO ACUERDOS | AUDIO LIBRO

México sera potencia en generación de hidrógeno verde

DESCARGAR INTRODUCCIÓN AL ÁLGEBRA KOSTRIKIN PDF

UPIIP IPN | CAMPUS PALENQUE

EL HOMBRE EN BUSCA DE SENTIDO | AUDIO LIBRO

EL METABOLISMO CELULAR | BIOLOGÍA

LA HIPÉRBOLA | MATEMÁTICAS

LA HIPÉRBOLA | MATEMÁTICAS