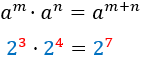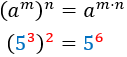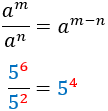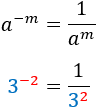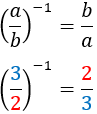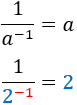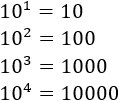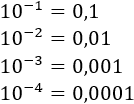- EJEMPLOS DE POTENCIAS Y RAÍCES | CURSO ONLINE de MATEMÁTICAS.
- EJEMPLOS DE POTENCIAS Y RAÍCES | CURSO ONLINE de MATEMÁTICAS
- 2. Propiedades de las potencias
- 3. Bases negativas
- 4. Potencias de 10
- 5. Exponentes negativos
- 6. 25 ejercicios resueltos de potencias y raíces matemáticas
- Primera potencia:
- Segunda potencia:
- EJEMPLOS DE POTENCIAS Y RAÍCES MATEMÁTICAS – Preguntas frecuentes
EJEMPLOS DE POTENCIAS Y RAÍCES | CURSO ONLINE de MATEMÁTICAS.
EJEMPLOS DE POTENCIAS Y RAÍCES MATEMÁTICAS
EJEMPLOS DE POTENCIAS Y RAÍCES | CURSO ONLINE de MATEMÁTICAS
Recordemos el concepto de potencia, las potencias con base y/o exponente negativo, las potencias de base 10 y las propiedades de las potencias. Después, resolvemos 25 ejercicios de potencias: calcular y simplificar expresiones algebraicas que involucran potencias.
Contenido de EJEMPLOS DE POTENCIAS Y RAÍCES
- Introducción
- Propiedades de las potencias
- Bases negativas
- Potencias de 10
- Exponentes negativos
- 25 ejercicios resueltos: calcular y simplificar potencias
1. Introducción a EJEMPLOS DE POTENCIAS Y RAÍCES MATEMÁTICAS
Introducción a las potencias: definición y ejemplos.
La potencia de base a y exponente b es la expresión algebraica
Esta potencia representa la multiplicación de la base, a, por sí misma tantas veces como indica el exponente, b:
Leemos la potencia
como a elevado a b.
Veamos algunos ejemplos:
Ejemplos de potencias matemáticas
-
Potencia 4 elevado a 2 ó 4 al cuadrado:
-
Base: 4. Exponente: 2.
-
Potencia 3 elevado a 3 ó 3 al cubo:
-
Base: 3. Exponente: 3.
-
Potencia 2 elevado a 4 ó 2 a la cuarta:
-
Base: 2. Exponente: 4.
-
Potencia -3 elevado a 2 ó -3 al cuadrado:
-
Base: -3. Exponente: 2.
Casos especiales:
-
Un número elevado a es
-
Un número elevado a es ……..
-
Un número elevado a es su inverso, …….
2. Propiedades de las potencias
Veamos las propiedades básicas de las potencias (no incluimos las de las potencias que representan raíces, es decir, las que tienen una fracción en el exponente):
| Producto
|
Potencia
|
| Cociente
|
Exponente negativo
|
| Inverso
|
Inverso
|
Nota: a la hora de aplicar las propiedades del producto y del cociente de potencias, no olvidemos que las bases de las potencias tienen que ser iguales.
3. Bases negativas
Potencias con base negativa.
Una potencia con base positiva siempre es positiva. Por ejemplo,
Cuando la base es negativa, el signo depende de la paridad del exponente (es decir, de si es par o impar):
-
Si el exponente es par, el resultado es positivo.
Por ejemplo,
-
Si el exponente es impar, el resultado es negativo.
Por ejemplo, y
El porqué es sencillo: cuando el exponente es par, podemos agrupar sus factores de dos en dos, siendo positivos estos productos. Por ejemplo,
Si el exponente es impar, queda un factor negativo que no podemos agrupar:
Importante:
Cuando una base es negativa, siempre tenemos que escribirla entre paréntesis. Si no hay paréntesis, se considera que el signo negativo está delante de la potencia, no en la base, cambiando el signo del resultado de la potencia.
Por ejemplo,
La base de la potencia es
La base de la potencia es
4. Potencias de 10
Potencias con base 10.
Una potencia cuya base es 10 es muy fácil de calcular: el exponente indica el número de 0’s del resultado, delante o detrás del número 1:
-
Si el exponente es negativo, los 0’s van detrás del 1:

-
Si el exponente es positivo, los 0’s van delante del 1:

Más información y problemas: Notación científica.
5. Exponentes negativos
Potencias con exponente negativo.
Ya hemos visto que la potencia con exponente
es el inverso de la base:
Si aplicamos la propiedad potencia de una potencia, tenemos
Por ejemplo,
6. 25 ejercicios resueltos de potencias y raíces matemáticas
Tenemos tres tipos de ejercicios:
- Primero, calculamos potencias básicas.
- Después, calculamos potencias aplicando sus propiedades.
- Finalmente, simplificamos expresiones algebraicas con potencias, pudiendo haber parámetros.
1.Ejercicio
Calcular la potencia dos elevado a cinco:
![]()
La base es 2 y el exponente es 5.
Aplicamos la definición de potencia, es decir, multiplicamos la base, 2, por sí misma tantas veces como indica el exponente, 5:
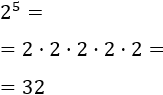
2.Ejercicio
Calcular las siguientes potencias:
![]()
3.Ejercicio
Calcular las siguientes potencias:
![]()
Las potencias de son ó . El resultado de la primera potencia es
porque el exponente es impar:
![]()
El resultado de la segunda potencia es porque, aunque el exponente sea par, el signo negativo no está en la base, sino multiplicando la potencia:
![]()
La base de la primera potencia es y la de la segunda es
4.Ejercicio
Calcular 0,5 al cuadrado:
![]()
La base es un número decimal, pero sus potencias se calculan del mismo modo:
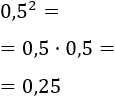
5.Ejercicio
Calcular la potencia dos elevado a menos tres:
![]()
Como el exponente es negativo, primero escribimos la potencia como una fracción: el numerador es 1 y el denominador es la potencia sin el signo negativo del exponente. Luego, calculamos la potencia del denominador:
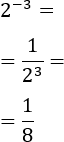
6.Ejercicio
Calcular la potencia cuyo exponente es menos tres y cuya base es la potencia dos al cuadrado:
![]()
Tenemos la potencia de una potencia. Por tanto, multiplicamos ambos exponentes y mantenemos la base. No olvidemos el signo negativo del exponente:
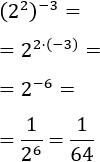
Hemos escrito la potencia como una fracción para eliminar el signo negativo del exponente.
7.Ejercicio
Calcular el siguiente cociente de potencias con la misma base:
![]()
Como las bases de las potencias son iguales, la regla dice que se restan los exponentes (el del numerador menos el del denominador). Se obtiene un exponente negativo:
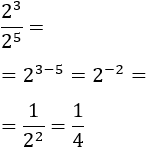
8.Ejercicio
Calcular el producto de potencias de :
![]()
Como tenemos una multiplicación de potencias con la misma base, sumamos sus exponentes:
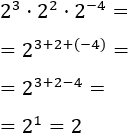
9.Ejercicio
Calcular el siguiente producto de potencias:
![]()
Tenemos una multiplicación de cuatro potencias. Dos de ellas tienen base
y las otras dos tienen base
. Sumamos los exponentes de las potencias con base común:
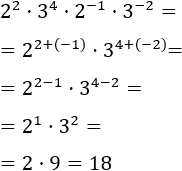
10.Ejercicio
Calcular el producto de potencias:
![]()
La base de las tres potencias son distintas, pero el número
se puede escribir como un producto:
. Al hacer este cambio, ya tendremos algunas bases comunes:
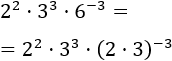
Aplicamos la propiedad de la potencia de un producto:
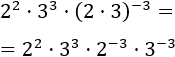
Ahora, sumamos los exponentes de las bases comunes:
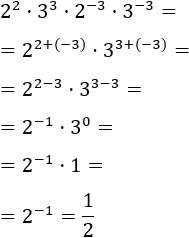
11.Ejercicio
Calcular el cociente de productos de potencias:
![]()
Como tenemos una división, restamos los exponentes del denominador a las potencias con igual base:
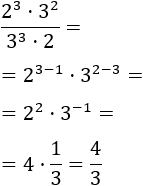
12.Ejercicio
Calcular el cociente de potencias:
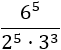
Escribimos el como el producto
y aplicamos la propiedad de la potencia de una producto. Después, restamos los exponentes del denominador:

13.Ejercicio
Calcular la siguiente división de un producto de potencias:
![]()
Sumamos los exponentes del numerador y restamos los exponentes de los denominadores a las potencias con igual base:
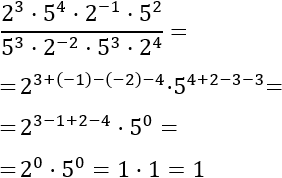
14.Ejercicio
Calcular las siguientes operaciones entre potencias con bases distintas:
![]()
Tenemos un producto de potencias en el numerador (bases 2 y 3) y una potencia con base 6 en el denominador, pero no podemos aplicar las propiedades porque las bases son distintas (2, 3 y 6).
Para poder aplicar las propiedades, escribimos el número 6 como la potencia porque, de este modo, tendremos algunas bases comunes:
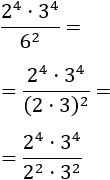
Hemos aplicado la potencia de un producto.
Ahora, restamos los exponentes de las bases comunes:
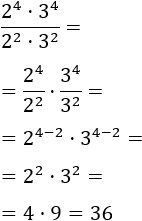
15.Ejercicio
Calcular las siguientes potencias negativas cuyas bases son fracciones:
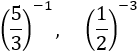
El exponente negativo es el inverso de la base. En el caso de una fracción, su inverso se calcula cambiando numerador por denominador:
Primera potencia:
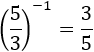
Segunda potencia:
Podemos ver la potencia como la potencia de una potencia (el cubo del inverso):
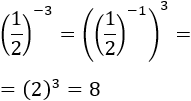
16.Ejercicio
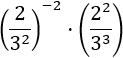
Primero podemos eliminar el signo negativo del exponente de la primera potencia escribiendo la inversa de la fracción. Después, aplicamos las propiedades del producto, cociente y potencia de una potencia.

17.Ejercicio
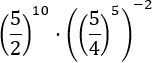
Aplicamos las reglas de las potencias a cada una de ellas para simplificar la expresión. Transformamos la base en la potencia para tener bases comunes:
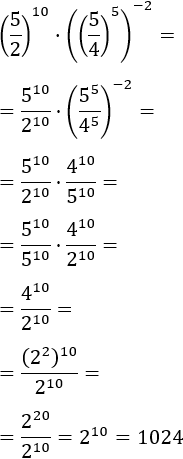
18.Ejercicio
![]()
La dificultad de esta expresión es que tenemos tres bases distintas. Para solucionarlo, descomponemos cada una de ellas como un producto de potencias de primos.
Escribiremos
Después, sólo tenemos que multiplicar o dividir potencias con bases comunes:

19.Ejercicio
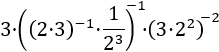
Aplicamos las propiedades de las potencias como en los ejercicios anteriores, pero primero en los interiores de los paréntesis para que ir reduciéndolos hasta eliminarlos:
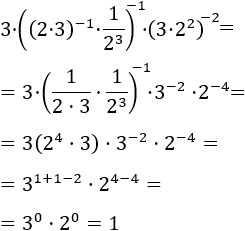
20.Ejercicio
Calcular:
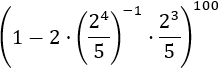
Tenemos un exponente muy alto, pero no debemos preocuparnos por ello. Lo importante de este ejercicio es que la base de la potencia, que es todo el paréntesis, es una resta y no tenemos reglas para desarrollarla. Por tanto, tenemos que trabajar en el interior del paréntesis hasta poder aplicar las reglas:
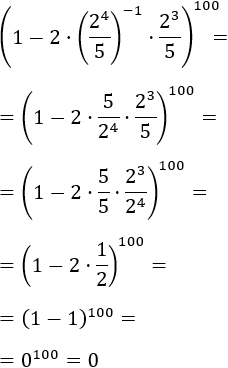
Nota: las potencias de 0 son 0 porque
21.Ejercicio
Calcular:
![]()
El único problema de este ejercicio es la potencia de base 18, pero podemos escribir 18 como
Después, aplicamos las propiedades:
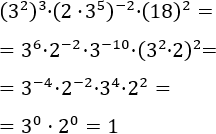
22.Ejercicio
Simplificar:
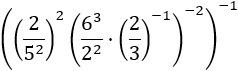
Tenemos muchos exponentes. Aplicamos las reglas poco a poco. Nosotros lo haremos desde fuera hacia dentro:
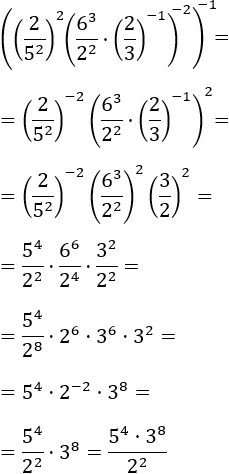
23.Ejercicio
Calcular:
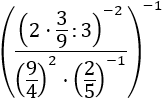
24.Ejercicio
Calcular:
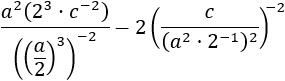
La dificultad de esta expresión son los parámetros, es decir, las letras. Se trabaja con ellas del mismo modo que con los números (los parámetros representan números).
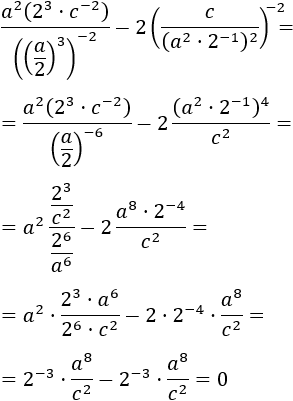
25.Ejercicio
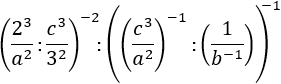
Aunque es simplemente una cuestión de notación, escribiremos las divisiones “:” en forma de fracciones “/”.
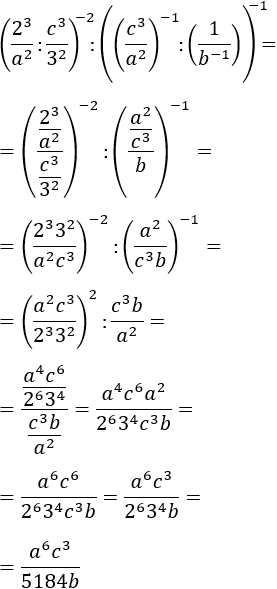
EJEMPLOS DE POTENCIAS Y RAÍCES MATEMÁTICAS – Preguntas frecuentes