CALCULO INTEGRAL MATEMÁTICAS | CURSO ONLINE .

CALCULO INTEGRAL | CURSO ONLINE DE MATEMÁTICAS.

Función integrable en un intervalo cerrado.

Partición de un intervalo cerrado:

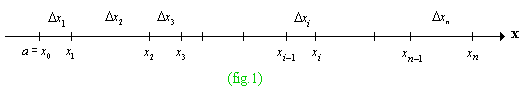
Suma de Riemann:

Teoremas que justifican las propiedades de la integral de una función.

El teorema fundamental del cálculo

El teorema fundamental del cálculo aclara la relación entre las derivadas y las integrales. La integración realizada en una función puede revertirse por la diferenciación.

El teorema fundamental del cálculo

Si una función f(x)  se define por el intervalo  [a,b] y si F(x)  es la antiderivada de f  en [a,b] , entonces

∫abf(x)dx=F(b)−F(a)=F(x)|ba

Podemos utilizar la relación entre diferenciación e integración descrita en el teorema fundamental del cálculo para calcular integrales definidas más rápidamente.

Ejemplo A

Calcula ∫12x2dx .

Solución:

Esta integral nos dice que debemos calcular el área bajo la curva f(x)=x2 , la cual es una parábola, sobre el intervalo [1, 2], como lo muestra la siguiente figura.

Para calcular la integral de acuerdo el teorema fundamental del cálculo necesitamos encontrar la antiderivada f(x)=x2 . Lo que resulta en F(x)=(13)x3+C , donde C es una constante de integración. ¿Cómo podemos obtener esto? Piensa en las funciones que tienen derivadas de x2 . Toma la derivada de  F(x) para comprobar que encontramos tal función.

Al sustituir en el teorema fundamental,

∫abf(x)dx∫12x2dx=F(x)∣∣ba=[13x3+C]21=[13(2)3+C]−[13(1)3+C]=[83+C]−[13+C]=73+C−C=73

Entonces, el área bajo la curva es (73)units2 .

LA INTEGRAL | CURSO ONLINE DE MATEMÁTICAS

Integral inmediata.

Se conoce como integrales inmediatas a todas aquellas funciones que tienen una fórmula directa para resolverse. Su solución es inmediata pues se trata sólo de sustituir los valores de acuerdo a la fórmula correspondiente y realizar las operaciones pertinentes.

Se presentan 3 tipos de integrales inmediatas:

1. Algebraicas.

2. Trigonométricas.

3. Logarítmicas o exponenciales.

LA INTEGRAL | CURSO ONLINE DE MATEMÁTICAS

Tabla de fórmulas de integración.

VER >>> AQUÍ

Métodos de integración.

Método de sustitución

Uno de los dos procedimientos más habituales para la resolución de integrales complicadas es el llamado método de sustitución o de cambio de variable. Esta técnica consiste en introducir una nueva variable t para sustituir a una expresión apropiada del integrando, de manera que la expresión resultante sea más fácil de integrar. Por ejemplo, la integral:

 

 

se simplifica notablemente si se aplica el cambio t = sen x. Entonces, se cumpliría que dt = cos x dx, con lo que la integral quedaría reducida a:

 

 

Finalmente se desharía el cambio de variable, con lo que el resultado final sería:

Integración por partes

El método de la integración por partes se emplea para simplificar el cálculo de la integral de un producto de funciones que puedan interpretarse como del tipo u (x) × v¿ (x). La fórmula de la integración por partes es la siguiente:

 

 

Este método resulta indicado particularmente cuando v × du es más fácil de integrar que u × dv.

Cálculo de áreas

La integral de una función continua entre los dos extremos de un intervalo [a, b] y tal que f (x) ³ 0 “ x Î [a, b] coincide con el área comprendida entre dicha función, el eje horizontal y las dos rectas que delimitan los intervalos, de ecuaciones x = a y x = b.

Este principio puede servir también para calcular las áreas comprendidas entre curvas, por simples operaciones aritméticas de adición y sustracción.

La integral de f (x) en el intervalo [a, b] coincide con el valor del área R.

Por convenio, dicha área se dice que es positiva cuando f (x) ³ 0 en el intervalo, y negativa si f £ 0 en [a, b]. Cuando la función tiene signo variable, las partes de la misma situadas por encima del eje horizontal añadirán valor positivo al área global, y las que discurran por debajo sumarán valores negativos a la misma.

Áreas formadas por dos curvas. Por consideraciones geométricas, el área de la intersección se calcula restando a la integral de f (x) en el intervalo [-1, 1] el valor de la integral de g (x) para ese mismo intervalo.

Integración numérica

En ocasiones, el cálculo de una integral definida en un intervalo resulta tan complicado que se hace casi irresoluble. En estos casos, se puede aplicar un método de integración numérica aproximada, consistente en dividir el intervalo de definición en un conjunto de subintervalos iguales, de manera que se trazan sus imágenes sobre la curva y se unen todos puntos imagen mediante segmentos rectilíneos.

Siendo f (x) la función de origen, y [a, b] el intervalo de integración, que se puede dividir en n subintervalos iguales de amplitud h tales que a = x0 < x1 < x2 < ¿ << xn = b, la región limitada por la curva de f (x) puede obtenerse aproximadamente a partir de la siguiente expresión:

 

 

Esta ley se llama regla de los trapecios. Evidentemente, cuanto mayor es el número de intervalos escogido, más cerca estará el valor obtenido del área real situada bajo la curva.

Aproximación del área de una función por integración numérica.

LA INTEGRAL | CURSO ONLINE DE MATEMÁTICAS

Integral definida y su notación.

La integral definida es un límite. Este límite puede calcularse con las fórmulas de integración inmediata. Para calcular el valor de la integral definida evaluamos primero el límite superior y después el límite inferior. La diferencia entre estos valores es el valor de la integral definida.

Ejemplo

Calcula la integral definida:

y representa geométricamente el resultado.

Calculamos la integral:

Ahora evaluamos:

Este resultado representa el área bajo la curva , desde hasta y sobre el eje . El cálculo de esta integral definida también se puede realizar utilizando la definición:

Preguntas frecuentes del CALCULO INTEGRAL | CURSO ONLINE DE MATEMÁTICAS.