¿QUE ES EL BINOMIO DE NEWTON? | MATEMÁTICAS
¿QUE ES EL BINOMIO DE NEWTON? | MATEMÁTICAS
Binomio de Newton, números combinatorios y el triángulo de Pascal.
Si has llegado hasta aquí es porque seguramente hay algún ejercicio que no sabes resolver y necesitas clases de matemáticas online. Si después de leer esto, quieres que te ayude a resolverlo o que te despeje alguna duda, puedes hacer dos cosas: o seguir buscando por Internet o contactar conmigo e ir directo al grano y ahorrarte tiempo.
Lo que vas a leer es tan sólo un ejemplo de lo que puedo enseñarte con mi método para enseñar matemáticas. Puedo explicarte paso a paso cualquier duda que no entiendas:
Binomio de Newton
El binomio de Newton es una fórmula que sirve para calcular cualquier potencia de un binomio (a+b).
Sabemos que para calcular la potencia de un binomio al cuadrado utilizamos las fórmulas de los productos notables, pero si tenemos que calcular por ejemplo un binomio elevado a 5, la cosa ya se complica.
Tendríamos que factorizar la potencia previamente en potencias de 2, luego ir desarrollando los cuadrados e ir multiplicando los polinomios resultantes dos a dos:
![]()
Se puede resolver así, pero hay que realizar muchas operaciones, con el tiempo que conlleva y el riesgo a cometer algún fallo. Y cuanto mayor sea el exponente al que está elevado el binomio, todavía hay que hacer más operaciones, siendo una tarea casi imposible si el exponente es demasiado elevado.
Por tanto, las potencias de un binomio las vamos a calcular mediante la fórmula del binomio de Newton, que es lo que veremos a continuación.
Fórmula del binomio de Newton
Con la fórmula del binomio de Newton podemos calcular la potencia de un binomio elevado a cualquier exponente y es la siguiente:

Cuando los términos del binomio se están restando, en el desarrollo se van alternando signos más y signos menos:
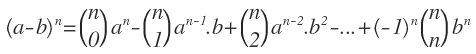
La fórmula a priori parece difícil, pero vamos a ver un ejemplo, que analizaremos más despacio para que la puedas entender mejor.
Vamos a calcular la potencia de un binomio (a+b) elevado a 5:
![]()
Aplicamos la fórmula sustituyendo n por 5 en este caso y operando en los exponentes y nos queda la siguiente expresión:

El desarrollo de la potencia no está terminada, pero antes de seguir, vamos a analizar esta expresión detenidamente.
- El número de términos del desarrollo es n+1. En nuestro caso, como estamos elevando el binomio a 5, y por tanto n=5, tenemos 5+1=6 término.
- Los coeficientes de cada término del desarrollo son números combinatorios (que veremos en el siguiente apartado qué son y cómo se resuelven), donde el número de arriba es igual al exponente del binomio (en nuestro caso 5) y el número de abajo va aumentando de 1 en 1 desde 0 hasta el valor del exponente n (en nuestro caso desde 0 hasta 5):
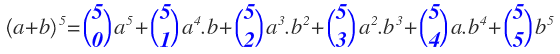
- Los exponentes del primer término (en nuestro caso a) van disminuyendo desde n hasta 0 (en nuestro caso, desde «a» elevado a 5, hasta el último término que no aparece «a» porque «a» elevado a 0 es 1):

- Los exponentes del segundo término (en nuestro caso b) van aumentando desde 0 hasta hasta (en nuestro caso, desde «b» elevado a 0, que es 1 y no aparece, hasta «b» elevado a 5):
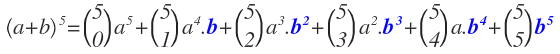
- La suma de los exponentes en cada término es igual a n. En nuestro caso, en cada término los exponentes siempre suman 5.
Visto esto vamos a ver cómo podemos calcular el valor de los números combinatorios
Números combinatorios
El número de combinaciones sin repetición de n elementos tomados de r en r también se llama número combinatorio y se calcula mediante la siguiente fórmula:

Se lee n sobre r y se representa uno sobre otro entre paréntesis, quedando la n arriba y la r abajo.
Por ejemplo, vamos a aplicar la fórmula anterior para resolver 5 sobre 2:
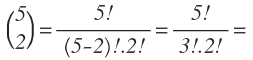
Desarrollamos el factorial del numerador hasta llegar al mayor factorial del denominador, que en este caso es 3!, y los anulamos:

Desarrollamos el factorial que nos queda en el denominador y operamos:

Aplicando la fórmula de los números combinatorios, puede ser una forma de resolverlos en el desarrollo del binomio de Newton, pero vamos a ver otra forma todavía más sencilla en el siguiente apartado.
El triángulo de Pascal
Un matemático llamado Pascal (aunque hay libros que se lo atribuyen a Tartaglia) construyó un triángulo de números combinatorios, colocando por filas los números combinatorios, de manera que en cada fila, el número superior de los números combinatorios coincide con el número de la fila y el número inferior de los números combinatorios va aumentando desde 0 hasta el número de fila.
Por tanto, en la primera fila hay 2 números combinatorios (número inferior desde 0 hasta 1), en la segunda fila hay 3 números combinatorios (número inferior desde 0 hasta 2) y así sucesivamente:
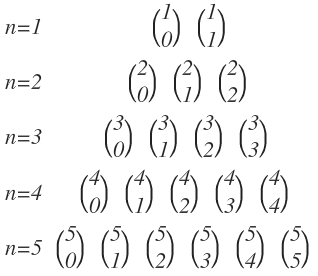
Si calculamos cada uno de los números combinatorios, el triángulo de Pascal nos queda de la siguiente manera:

Donde se puede observar las siguientes propiedades:
Propiedades del triángulo de Pascal
- Todas las filas empiezan y terminan por 1
- Todas las filas son simétricas
- Cada número se obtiene sumando los dos números que tiene encima, excepto los extremos que siempre son 1.
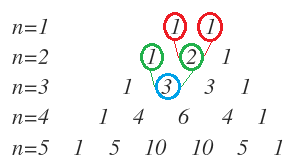
Por tanto, para construir el triángulo de Pascal, no es necesario ir calculando cada número combinatorio, sino que se colocan los 1 de los extremos y luego se van añadiendo los números de arriba a abajo, resultado de sumar los dos números que quedan por encima.
Volviendo al binomio de Newton, si te das cuenta, los números combinatorios que queda, corresponden a los números combinatorios de una de las filas de triángulo de Pascal, en nuestro caso a la fila de n=5:

Por tanto, para obtener el valor de los números combinatorios, sólo tenemos que sustituir cada número combinatorio por su valor, que lo encontramos en la fila 5:
![]()


[…] 2.1 Binomio de Newton […]
[…] 2.1 Dar click ▷ Binomio de Newton […]