- LIMITES DE UNA FUNCIÓN | MATEMÁTICAS
- PREGUNTAS FRECUENTES SOBRE EL LIMITE DE UNA FUNCIÓN
- Concepto intuitivo.
- Definición formal del limite de una función.
- Teoremas sobre límites.
- Límite de una Constante:
- Límite de una Constante por una Función:
- Límite de la suma de funciones:
- Límite de la resta de funciones:
- Límite de la multiplicación o producto de funciones:
- Límite de la división o cociente de funciones:
- Límite de la potencia:
- Límite de la raíz:
- Límite del logaritmo:
- Límite de la función de otra función:
- Obtención de límites.
- Formas indeterminadas.
- Continuidad en un punto y en un intervalo.
LIMITES DE UNA FUNCIÓN | MATEMÁTICAS
LIMITES DE UNA FUNCIÓN | MATEMÁTICAS
PREGUNTAS FRECUENTES SOBRE EL LIMITE DE UNA FUNCIÓN
Un punto a sobre el eje de las x. Un punto L sobre el eje de las y. Y una función f con valores reales de variable real, que puede o no estar definida en a.
LIMITES DE UNA FUNCIÓN | MATEMÁTICAS
Concepto intuitivo.
Cuando se trabaja con funciones frecuentemente nos interesa averiguar el comportamiento de una determinada función cuando la variable independiente, x, se aproxima a un determinado valor, a. En otras palabras: queremos averiguar si la función se aproxima a un determinado valor, b, aumenta indefinidamente, disminuye indefinidamente o no tiene un comportamiento claramente definido.
Podría pensarse que para averiguar esa cuestión bastaría con calcular el valor de la función en el punto que se está considerando, es decir calcular f(a). Sin embargo, en muchos casos ese cálculo no responde a la pregunta que nos hacemos por diferentes motivos:
Algunas veces a no pertenece al dominio de la función, pero se encuentra en su borde; por lo tanto enese caso no es posible calcular f(a) pero sí tiene sentido interesarse por el comportamiento de la función en las cercanías de a.
En otras ocasiones a pertenece al dominio de la función, pero el comportamiento de la función cerca de a difiere bastante del valor de f(a).
Puede suceder también que el comportamiento de la función sea diferente a la izquierda y a la derecha del punto a.
LIMITES DE UNA FUNCIÓN | MATEMÁTICAS
Definición formal del limite de una función.
En esta sección vamos a formalizar el concepto intuitivo del límite de una función visto con anterioridad al concepto formal del límite de una función en términos de la aplicación de las tradicionales letras del alfabeto griego ε y δ en la definición del límite de una función, puesto que en la definición intuitiva del límite de una función se consideraron los términos imprecisos “f(x) está cercano de L”, siempre que “x está cercano de a”. Para precisar consideremos el límite de la función f(x)=2x+1 cuando x⟶3, es decir, limx→3(2x+1)=7 y contestemos la pregunta.
¿Qué tan cerca de 3 debe estar x, para que f(x) difiera de 7 una distancia menor de ε=0.5?
Teoremas sobre límites.
Los límites de una función presentan las siguientes propiedades:
Límite de una Constante:
El límite de una constante es la misma constante.
límx→x0 k = k
1.Ejemplo: límx→ 1 5 = 5
Límite de una Constante por una Función:
El límite de una constante por una función es igual a la constante por el límite de la función.
límx→x0 k · f(x) = k · límx→x0 f(x)
2.Ejemplo: límx→0 10·(x – 1)/(x + 1) = 10 · límx→0 (x – 1)/(x + 1) = 10 · (-1/1) = -10
Límite de la suma de funciones:
El límite de la suma de funciones es igual a la suma de los límites de las funciones por separado.
límx→x0 [ f(x) + g(x)] = límx→x0 f(x) + límx→x0 g(x)
3.Ejemplo: límx→ -2 (x + 2) + 1 / x = límx→ -2 (x + 2) + límx→ -2 1/x = 0 – 1/2 = -1/2
Límite de la resta de funciones:
El límite de la resta de funciones es igual a la resta de los límites de las funciones por separado.
límx→x0 [ f(x) – g(x)] = límx→x0 f(x) – límx→x0 g(x)
4.Ejemplo: límx→ -2 (x + 2) – 1 / x = límx→ -2 (x + 2) – límx→ -2 1/x = 0 + 1/2 = 1/2
Límite de la multiplicación o producto de funciones:
El límite de la multiplicación de funciones es igual a la multiplicación de los límites de las funciones por separado.
límx→x0 f(x) · g(x) = límx→x0 f(x) · límx→x0 g(x)
5.Ejemplo: límx→ 1 5x · (1 + x) = límx→ 1 5x · límx→ 1 (1 + x) = 5 + 2 = 7
Límite de la división o cociente de funciones:
El límite de la división de funciones es igual a la división de los límites de las funciones por separado.
límx→x0 f(x) / g(x) = límx→x0 f(x) / límx→x0 g(x)
6.Ejemplo: límx→ -2 (x + 2) / (x – 1) = límx→ -2 (x + 2) / límx→ -2 (x – 1) = 0 / (-3) = 0
Límite de la potencia:
El límite de la potencia es igual a la potencia de los límites de las funciones por separado.
7.Ejemplo: límx→ 1 5x(1+1/x) = límx→ 1 5x lím(1+1/x) = 52 = 25
Límite de la raíz:
El límite de la raíz n-ésima es igual a la raíz n-ésima del límite de la función.
8.Ejemplo: límx→ 5 √5x = √límx→ 5 5x = √25 = 5
Límite del logaritmo:
El límite del logaritmo es igual al logaritmo del límite de la función.
9.Ejemplo: límx→ 5 log10 10x = log10 límx→ 510x = log10 105 = 5
Límite de la función de otra función:
El límite de la función de otra función es igual a la función del límite.
10.Ejemplo:
g(x) = 5x
f(x) = x + 1
entonces límx→ 1 g[f(x)] = g (límx→ 1 (x + 1)) = g(2) = 5 · 2 = 10
LOS LIMITES | MATEMÁTICAS
Obtención de límites.
1. Sustitución
2. Factorización
3. Racionalización
Comprendamos estas técnicas de resolución una por una utilizando un problema de cálculo.
1. Sustitución
La sustitución es el más simple de los tres métodos. Este método no siempre funciona bien, por lo que no debe depender únicamente de este. La sustitución también puede resultar útil cuando se utilizan los otros dos métodos.
Método:
Sustituya el límite (valor de la variable) en la ecuación dada para acercarse a ese valor específico.
Simplifique la ecuación y obtenga el resultado de la función.
Resolvamos la siguiente ecuación si x se acerca a 3. Sustituya el valor de x en la ecuación.

= 6/2 = 3
2. Factorización
Si el método de sustitución no funciona para usted, entonces debería probar la factorización para resolver los límites. Este método también es sencillo como el primero porque es posible que ya haya aprendido la factorización en la escuela o la universidad.
Esto es lo que debe hacer con este método.
Método:
Haz los factores de numerador y denominador de la ecuación por separado.
Cancele la expresión en la ecuación si es posible.
Lleva la ecuación a la forma más simple.
Sustituye el valor de límite y simplifica.
Resolvamos el límite con factorización.

Factoriza el numerador.

Cancele, corte o divida el numerador y el denominador si es posible.

Ahora, sustituya y simplifique.

3. Racionalización
El método de racionalización es complejo en comparación con los dos métodos anteriores. Utilice este método si encuentra una raíz cuadrada en la ecuación.
Método:
• Toma el conjugado de la expresión.
• Simplifique la ecuación para obtener el valor final.
Resolvamos la siguiente función con racionalización.

Toma el conjugado.

Simplifica la ecuación anterior.

Sustituye el valor de x.

LOS LIMITES | MATEMÁTICAS
Formas indeterminadas.
La indeterminación
Para salvar indeterminaciones de este tipo, es posible reducir el cociente planteado a otro cuyo denominador no sea cero factorizando el numerador y/o el denominador, cancelando luego los factores comunes. En otras ocasiones, es posible crear un factor común multiplicando el numerador y el denominador por la expresión conjugada de la que se presenta en uno de ellos.
Ejemplo.
Halle ![]()
Al sustituir, resulta ![]() y
y ![]() lo que genera una indeterminación del tipo
lo que genera una indeterminación del tipo ![]() .
.
Sin embargo, como ![]() si x ¹ 3, resulta que la función
si x ¹ 3, resulta que la función ![]() coincide con la función (x + 3) salvo en x = 3.
coincide con la función (x + 3) salvo en x = 3.
Como interesa analizar el comportamiento de la función para valores de x próximos a 3 (por izquierda y por derecha), es posible determinar el comportamiento de ![]() analizando el de la función (x + 3).
analizando el de la función (x + 3).
Por lo tanto puede decirse que ![]()
La indeterminación
Los procedimientos algebraicos para salvar una indeterminación de este tipo, se desarrollan en los siguientes ejemplos:
Ejemplo.
Determine el valor de  .
.
Al reemplazar la variable por 2 resulta ¥ –¥ , que es una indeterminación.
Resolviendo la diferencia se obtiene:

![]()
Cuando x se aproxima a 2 por derecha, el numerador tiende a –3 y el denominador a 0 por valores mayores que él. Por lo tanto, la expresión resulta negativa y el límite es –¥.
![]() = –¥
= –¥
La indeterminación ![]()
Se analizará el límite del cociente de dos funciones polinomiales en el que la variable crece o decrece indefinidamente. Se debe tener en cuenta que el límite de una función polinomial de grado n ³ 1 cuando x tiende a +¥ ó a –¥ es +¥ ó –¥ . Para resolver límites de este tipo, se dividen el numerador y el denominador de la función dada por xn, siendo n el mayor de los grados de las funciones polinomiales. Luego se aplican las propiedades de los límites.
Ejemplo.
Halle 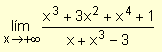
La función dada consiste en el cociente de dos funciones polinomiales: una de grado 4 y otra de grado 3. Por lo tanto, se dividen el numerador y el denominador por x4 y resulta:
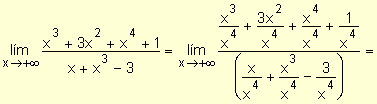
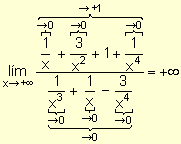
En el ejemplo dado, el grado de la función polinomial del numerador es mayor que el de la del denominador y se obtuvo en este caso ¥.
La indeterminación ![]()
Para salvar una indeterminación de este tipo, se pueden realizar distintos procedimientos algebraicos. Algunos de ellos se desarrollan en los siguientes ejemplos.
Ejemplo.
Halle ![]()
Cuando x ® –3, x2 + 6x +9 ® 0 y ![]() , por lo tanto
, por lo tanto ![]() , indeterminado.
, indeterminado.
Sin embargo, ![]() si x ¹ – 3.
si x ¹ – 3.
Por lo tanto: ![]()
LIMITES DE UNA FUNCIÓN | MATEMÁTICAS
Continuidad en un punto y en un intervalo.
¿Cuándo una función es continua? ¿Qué es una función continua?
Para empezar, una función es continua cuando está definida en todo su dominio, es decir, su domino es todo R.
En otras palabras, una función es continua cuando su gráfica se puede dibujar sin levantar el lápiz del papel
No obstante, en cierta funciones, como las que funciones definidas a trozos o funciones cuyo dominio no es todo R, en las que existen puntos críticos donde es necesario estudiar su continuidad.
Una función es continua en un punto X0 si existe el límite cuando la función tiende a ese punto y tiene un valor determinado y además, el valor de la función en ese punto es igual al valor del límite:
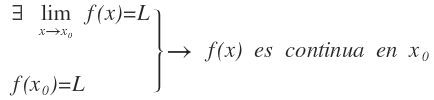
En las funciones definidas a trozos y en las funciones cuyo límite resulte una indeterminación de un número entre cero, para que exista el límite de la función en un punto, debemos calcular los límites laterales y éstos deben tener el mismo valor, es decir, el límite por la izquierda y por la derecha de ese punto deben coincidir:

Si no se cumple todo lo anterior, la función no será continua, es decir, si existe el límite pero no coincide con el valor de la función o no existe el límite en ese punto o la función en ese punto no existe, la función no será continua y por tanto, existirá uno de los tipos de discontinuidades que te voy a explicar en el siguiente apartado.
LIMITES DE UNA FUNCIÓN | MATEMÁTICAS


[…] 15. Límites […]